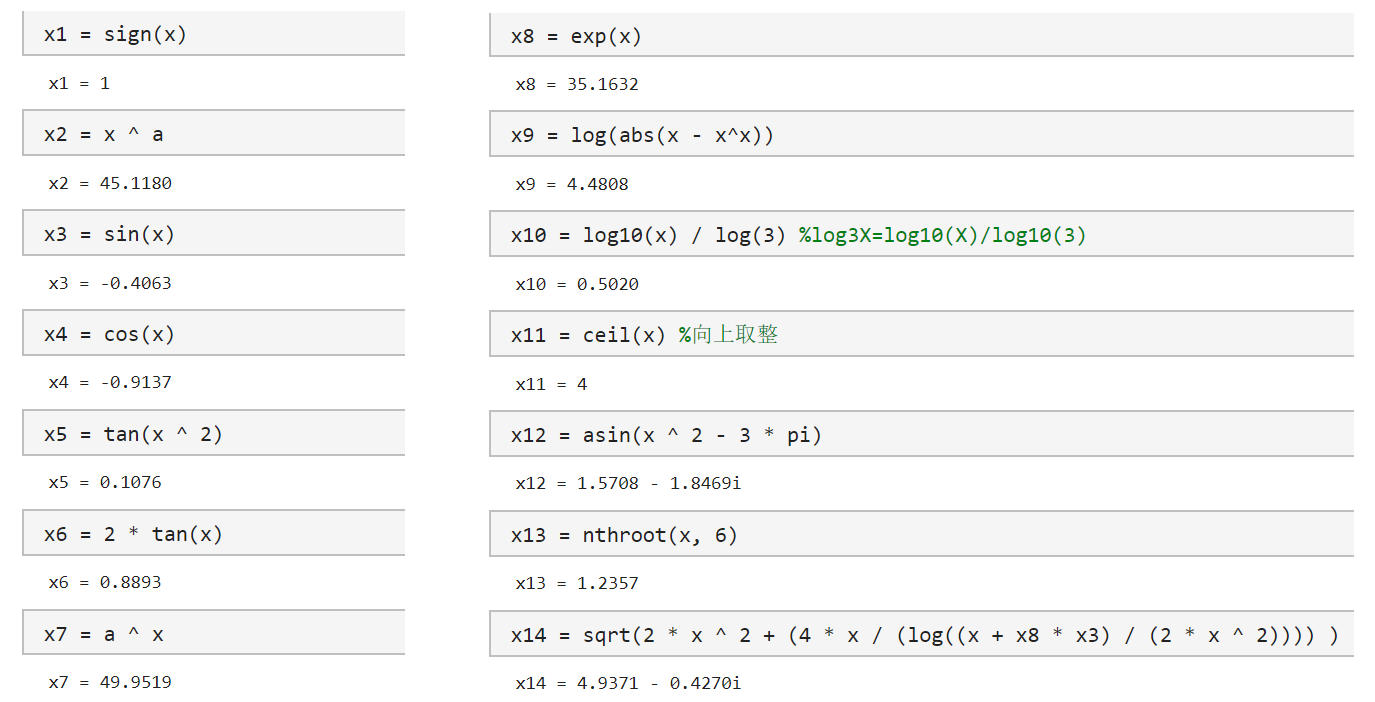
回忆你所学过的数学函数并给出 x=3.56 时以下函数的值
s i g n ( x ) , x a ( a = 3 ) , sin ( x ) , cos ( x ) , tan ( x 2 ) , 2 tan ( x ) \begin{aligned}sign\left( x\right) ,x^{a}\left( a=3\right) ,\sin \left( x\right) ,\cos \left( x\right) ,\tan \left( x^{2}\right) ,2\tan \left( x\right) \end{aligned} s i g n ( x ) , x a ( a = 3 ) , sin ( x ) , cos ( x ) , tan ( x 2 ) , 2 tan ( x )
a x ( a = 3 ) , e x , ln ( ∣ x − x x ∣ ) , log 3 x , [ x ] , arcsin ( x 2 − 3 π ) , x 6 , 2 x 2 + 4 x ln x + e x sin x 2 x 2 \begin{aligned}a^{x}\left( a=3\right) ,e^{x},\ln \left( \left| x-x^{x}\right| \right) ,\log _{3}x,\left[ x\right] ,\\
\arcsin \left( x^{2}-3\pi \right) ,\sqrt[6] {x},\sqrt{2x^{2}+\dfrac{4x}{\ln \dfrac{x+e^{x}\sin x}{2x^{2}}}}\end{aligned} a x ( a = 3 ) , e x , ln ( ∣ x − x x ∣ ) , log 3 x , [ x ] , arcsin ( x 2 − 3 π ) , 6 x , 2 x 2 + ln 2 x 2 x + e x sin x 4 x
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 x = 3.56 ; a = 3 ; x1 = sign (x) x2 = x ^ a x3 = sin (x) x4 = cos (x) x5 = tan (x ^ 2 ) x6 = 2 * tan (x) x7 = a ^ x x8 = exp (x) x9 = log (abs (x - x^x)) x10 = log10 (x) / log (3 ) x11 = ceil (x) x12 = asin (x ^ 2 - 3 * pi ) x13 = nthroot (x, 6 ) x14 = sqrt (2 * x ^ 2 + (4 * x / (log ((x + x8 * x3) / (2 * x ^ 2 )))) )
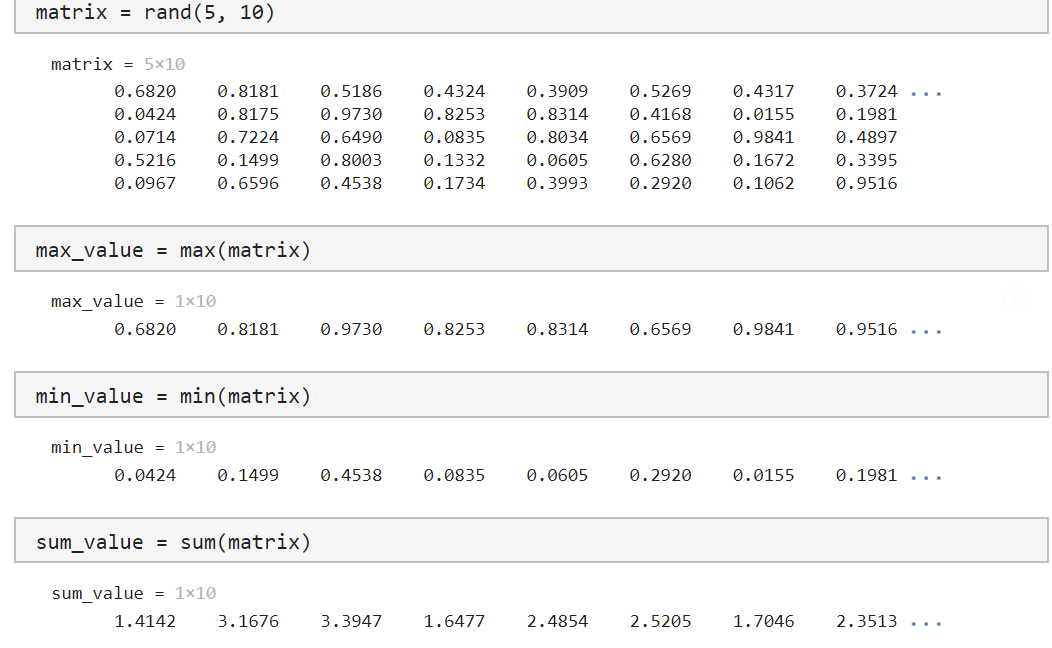
利用帮助了解向量函数 max,min, sum,mean,sort,length,矩阵函数 rand,size 的功能和用法。操作步骤:先用函数 rand 生成一个 5X10 的矩阵再使用上面提到的函数,看看产生什么样的输出。并用自己的话说明上述函数的功能和用法。
向量函数:
max:返回向量中的最大值。 用法:max (vector)
min:返回向量中的最小值。 用法:min (vector)
sum:返回向量中所有元素的总和。 用法:sum (vector)
mean:返回向量中所有元素的平均值。 用法:mean (vector)
sort:对向量进行排序,按升序排列。 用法:sort (vector)
length:返回向量中的元素个数。 用法:length (vector)
矩阵函数:
rand:生成指定大小的随机矩阵,元素值在 0 和 1 之间。 用法:rand (rows, columns)
size:返回矩阵的大小(行数和列数)。 用法:size (matrix)
1 2 3 4 5 6 7 8 9 10 11 12 13 matrix = rand (5 , 10 ) max_value = max (matrix) min_value = min (matrix) sum_value = sum(matrix) mean_value = mean (matrix) sorted_matrix = sort (matrix) matrix_length = length (matrix)
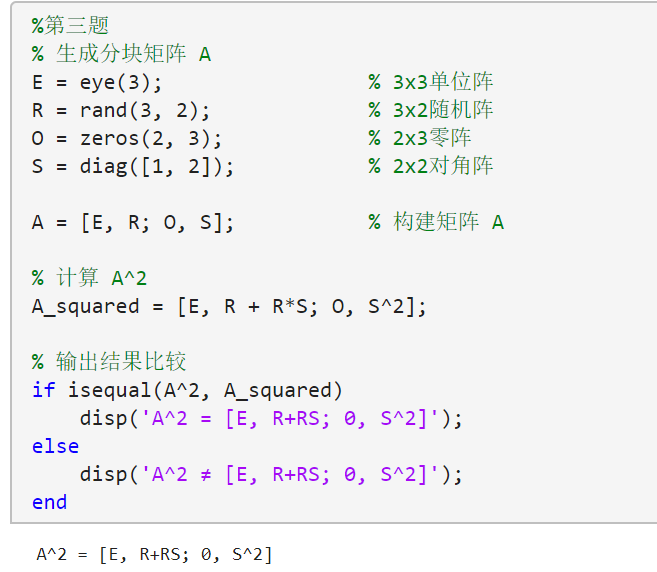
3. 设有分块矩阵 A = [ E 3 × 3 R 3 × 2 O 2 × 3 S 2 × 2 ] A=\begin{bmatrix}
E_{3\times 3} & R_{3\times 2} \\
O_{2\times 3} & S_{2\times 2}
\end{bmatrix} A = [ E 3 × 3 O 2 × 3 R 3 × 2 S 2 × 2 ] A 2 = [ E R + R S 0 S 2 ] A^{2}=\begin{bmatrix}
E & R+RS \\
0 & S^{2}
\end{bmatrix} A 2 = [ E 0 R + RS S 2 ] [ E R + R S 0 S 2 ] \begin{bmatrix}
E & R+RS \\
0 & S^{2}
\end{bmatrix} [ E 0 R + RS S 2 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 E = eye (3 ); R = rand (3 , 2 ); O = zeros (2 , 3 ); S = diag ([1 , 2 ]); A = [E, R; O, S]; A_squared = [E, R + R*S; O, S^2 ]; if isequal (A^2 , A_squared) disp ('A^2 = [E, R+RS; 0, S^2]' ); else disp ('A^2 ≠ [E, R+RS; 0, S^2]' ); end
在同一个坐标下作出 $y_{1}=x,y_{2}=x-\dfrac {x^{3}}{3!},y_{3}=x-\dfrac {x^{3}}{3!}+\dfrac {x^{5}}{5!},y_{4}=\sin \left ( x\right) $,这四条曲线的图形,说明 Taylor 公式说明了什么问题。
Taylor 公式是一种用无穷级数展开来逼近函数的方法。它可以将一个函数在某个点附近的局部行为用多项式来表示。y1 = x 就是函数 f (x) = x 在 x = 0 处的一阶泰勒展开式,y2 和 y3 分别是 f (x) = sin (x) 在 x = 0 处的三阶和五阶泰勒展开式。通过绘制这些曲线,我们可以观察到泰勒展开式在给定点附近的逼近效果。Taylor 公式说明了在某个点附近,一个光滑函数可以用一个多项式逼近。通过增加多项式的阶数,我们可以获得更高精度的逼近结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 x = linspace (-2 *pi , 2 *pi , 100 ); y1 = x; y2 = x - x.^3 /factorial (3 ); y3 = x - x.^3 /factorial (3 ) + x.^5 /factorial (5 ); y4 = sin (x); figure ;hold on;plot (x, y1, 'b' , 'LineWidth' , 2 );plot (x, y2, 'r' , 'LineWidth' , 2 );plot (x, y3, 'g' , 'LineWidth' , 2 );plot (x, y4, 'm' , 'LineWidth' , 2 );xlabel('x' ); ylabel('y' ); legend ('y_1 = x' , 'y_2 = x - x^3/3!' , 'y_3 = x - x^3/3! + x^5/5!' , 'y_4 = sin(x)' );title('Taylor公式的示例' ); hold off;
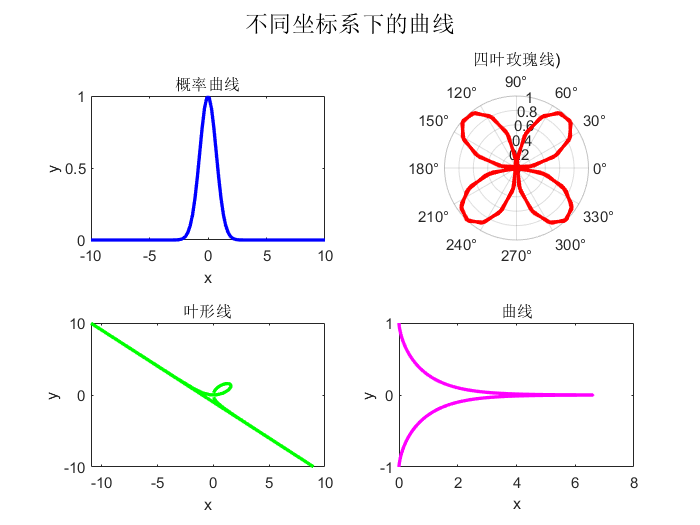
用 subplot 分别在不同的坐标系下作出四条曲线
(1) 概率曲线 y = e − x 2 y=e^{-x^{2}} y = e − x 2
(2) 四叶玫瑰线 $\rho =\sin 2\theta $
(3) 叶形线 { x = 3 t 1 + t 3 y = 3 t 2 1 + t 3 \begin{cases}x=\dfrac{3t}{1+t^{3}}\\
y=\dfrac{3t^{2}}{1+t^{3}}\end{cases} ⎩ ⎨ ⎧ x = 1 + t 3 3 t y = 1 + t 3 3 t 2
(4)x = ln 1 + 1 − y 2 y − 1 − y 2 x=\ln \dfrac{1+\sqrt{1-y^{2}}}{y}-\sqrt{1-y^{2}} x = ln y 1 + 1 − y 2 − 1 − y 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 t = linspace (-10 , 10 , 100 ); x1 = t; y1 = exp (-x1.^2 ); theta = t; rho = sin (2 *theta); x3 = 3 *t./(1 + t.^3 ); y3 = 3 *t.^2. /(1 + t.^3 ); y4 = linspace (-1 , 1 , 1000 ); x4 = log ((1 + sqrt (1 - y4.^2 ))./y4) - sqrt (1 - y4.^2 ); figure ;subplot(2 , 2 , 1 ); plot (x1, y1, 'b' , 'LineWidth' , 2 );xlabel('x' ); ylabel('y' ); title('概率曲线' ); subplot(2 , 2 , 2 ); polarplot(theta, rho, 'r' , 'LineWidth' , 2 ); title('四叶玫瑰线)' ); subplot(2 , 2 , 3 ); plot (x3, y3, 'g' , 'LineWidth' , 2 );xlabel('x' ); ylabel('y' ); title('叶形线' ); subplot(2 , 2 , 4 ); plot (x4, y4, 'm' , 'LineWidth' , 2 );xlabel('x' ); ylabel('y' ); title('曲线' ); sgtitle('不同坐标系下的曲线' );
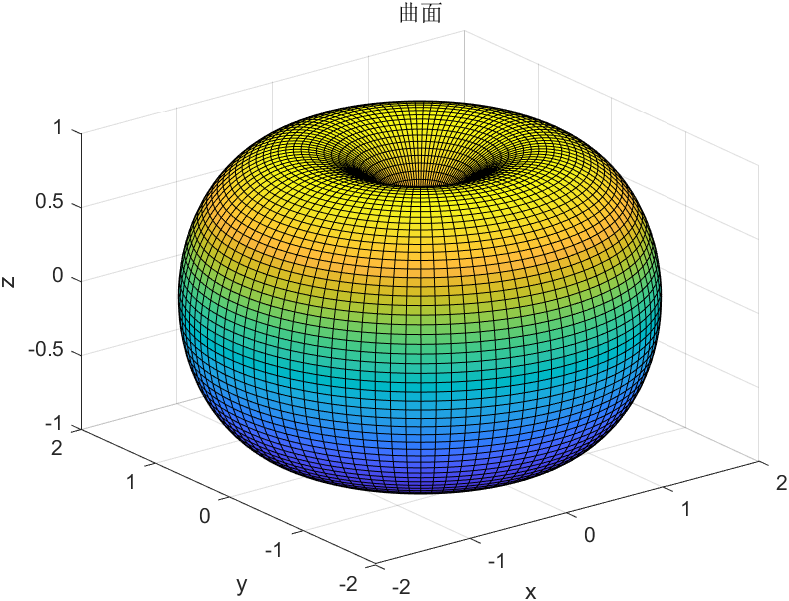
做出曲面 { x = ( 1 + cos u ) cos v , y = ( 1 + cos u ) sin v , u ∈ ( 0 , 2 π ) Z = sin u , v ∈ ( 0 , 2 π ) \begin{cases}x=\left( 1+\cos u\right) \cos v,\\
y=\left( 1+\cos u\right) \sin v,u\in \left( 0,2\pi \right) \\
Z=\sin u,v\in \left( 0,2\pi \right) \end{cases} ⎩ ⎨ ⎧ x = ( 1 + cos u ) cos v , y = ( 1 + cos u ) sin v , u ∈ ( 0 , 2 π ) Z = sin u , v ∈ ( 0 , 2 π )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 u = linspace (0 , 2 *pi , 100 ); v = linspace (0 , 2 *pi , 100 ); [u, v] = meshgrid (u, v); x = (1 + cos (u)) .* cos (v); y = (1 + cos (u)) .* sin (v); z = sin (u); figure ;surf(x, y, z); xlabel('x' ); ylabel('y' ); zlabel('z' ); title('曲面' );
利用 for 循环求 1! +2! +3!+ …+5! 的值。
153
1 2 3 4 5 6 7 8 9 n = 5 ; sum = 0 ; for k = 1 :n sum = sum + factorial (k); end disp (sum);
已知一维数组 A=[2,4,5,8,10],B=[4,6,9,3,4], 用 for 循环语句实现∑ i = 1 n A i B n − i + 1 \sum ^{n}_{i=1}A_{i}B_{n-i+1} ∑ i = 1 n A i B n − i + 1
153
1 2 3 4 5 6 7 8 9 10 11 12 A = [2 , 4 , 5 , 8 , 10 ]; B = [4 , 6 , 9 , 3 , 4 ]; n = length (A); result = 0 ; for i = 1 :n result = result + A(i ) * B(n - i + 1 ); end disp (result);