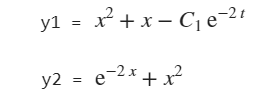6微分方程模型练习
- 用Matlab求解微分方程
matlab
1 | y1 = dsolve('Dy=-2*y+2*x.^2+2*x') |
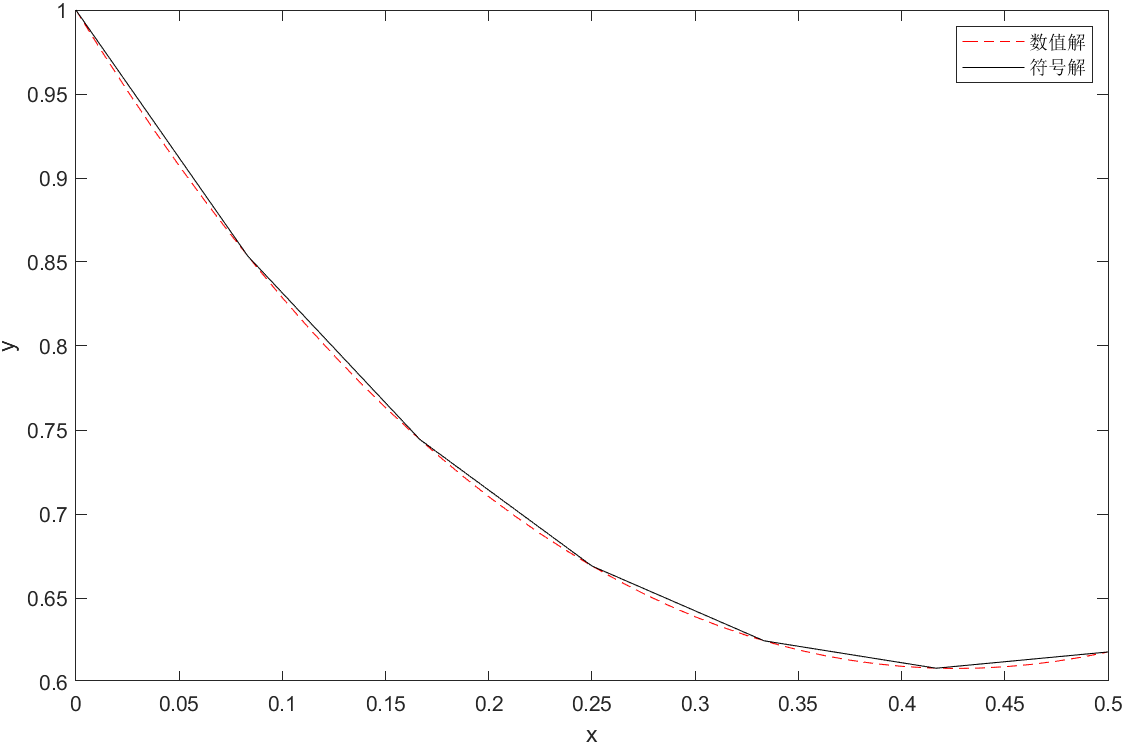
- 用Matlab分别求解微分方程,0≤x≤0.5的符号解和数值解;并在同一个图形界面上画出数值解和符号解的曲线。
matlab
1 | % 使用 ode45 求解微分方程 |
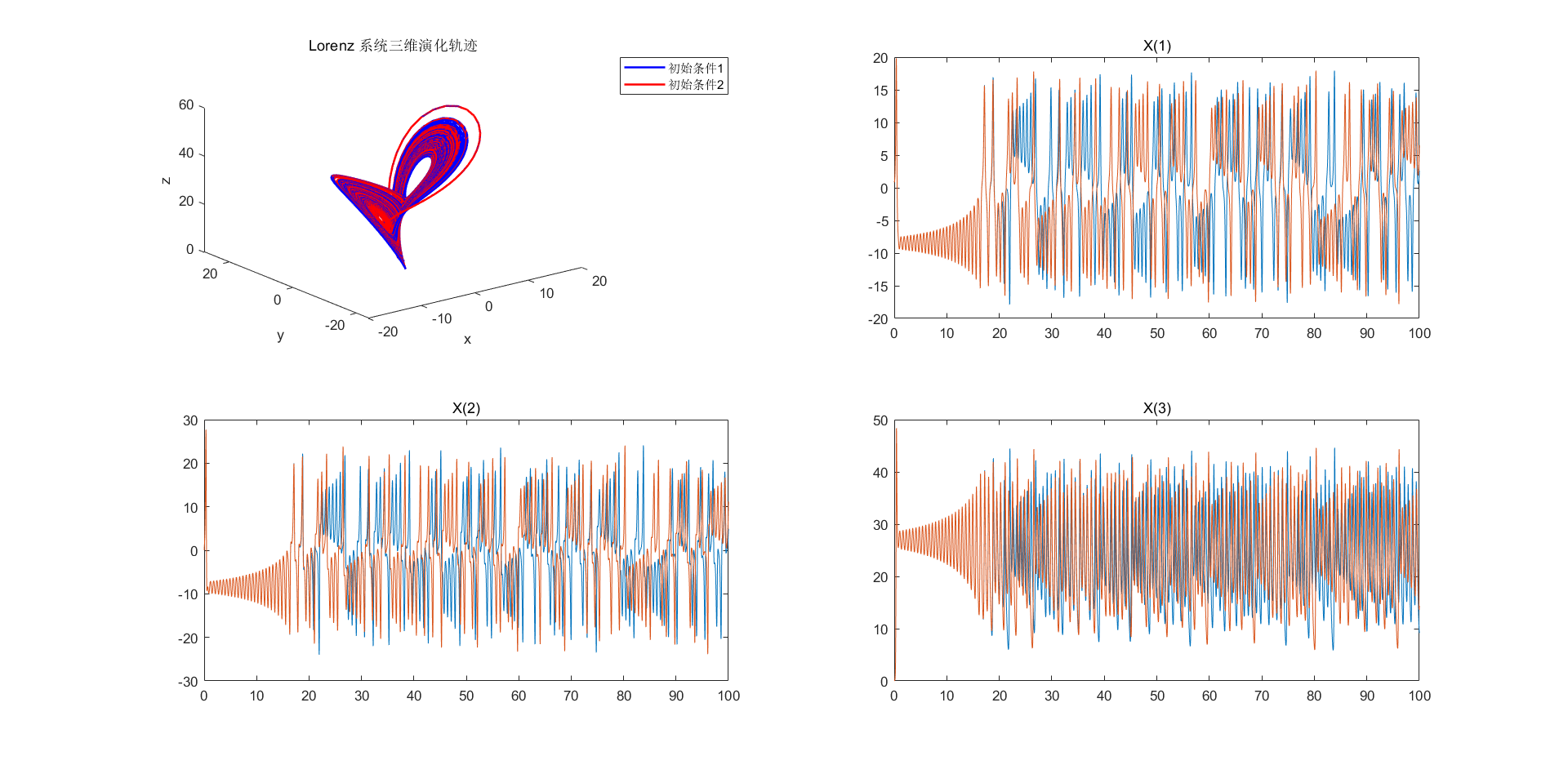
- 请运用 Matlab呈现Lorenz 模型系统的三维演化轨迹,并判断取值基本接近的两个不同初始条件对系统轨线演化的影响,由此分析该模型对初值的敏感性。
matlab
1 | % Lorenz 系统参数 |
初始条件微小变化会导致系统轨迹快速分离
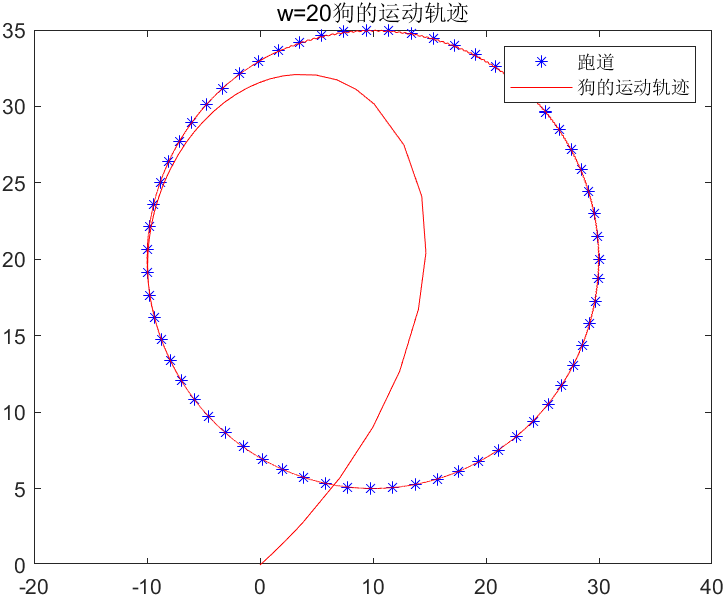
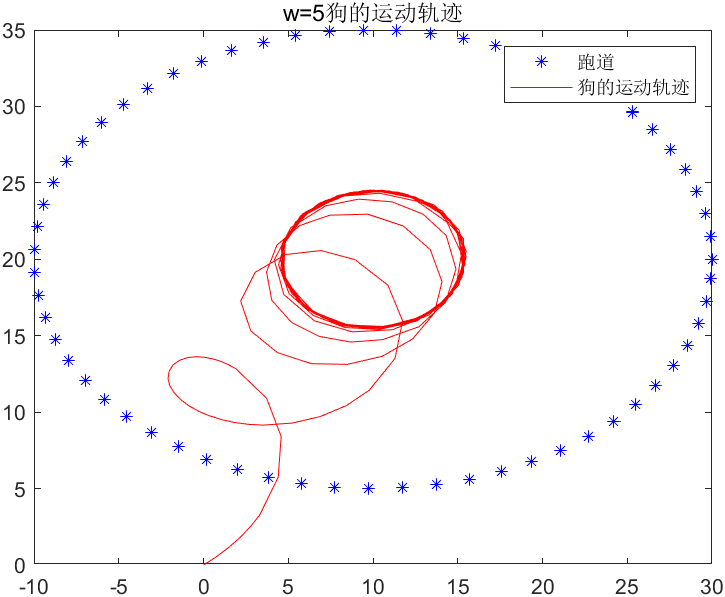
4.一个慢跑者在平面上按如下规律跑步:X=10+20cost,Y=20+15sint.突然有一只狗攻击他,这只狗从原点出发,以恒定速率w跑向慢跑者,狗运动方向始终指向慢跑者。分别求出w=20,w=5时狗的运动轨迹。
提示:
matlab
1 | clf; |
matlab
1 | function dy = f4(t,y) |
w = 20 时狗可以追上人,当w = 5时,狗不能追上人
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 知识小窝!