4模型规划练习

(0-1 规划)某公司董事会正在考虑几个大型的投资项目，每个项目只能投资一次，且各个项目所需的投资金额与能够产生的预期收益是不同的，具体见表 1 所示.已知公司现有的投资额是 1亿美金，其中投资项目 1和项目 2 是斥的，项目 3 和项目4 也是斥的此外如果不选择项目1或者项目 2，就不能选择项目 3、项目 4.投资项目 5、项目6 和项目7没有附加约束。董事会应该如何投资，使得预期收益最大?

投资项目	预计收益/百万美元	所需资金/百万美金
1	17	43
2	10	28
3	15	34
4	19	48
5	7	17
6	13	32
7	9	23

定义：Xi为是否投资项目，投资项目则x=1,不投资则x=0

模型：max = 17x1+10x2+15x3+19x4+7x5+13x6+9x7;

约束：资金约束：43x1+28x2+34x3+48x4+17x5+32x6+23x7<=100;

互斥约束：x1+x2<1;x3+x4<1;x3+x4<=x1+x2;

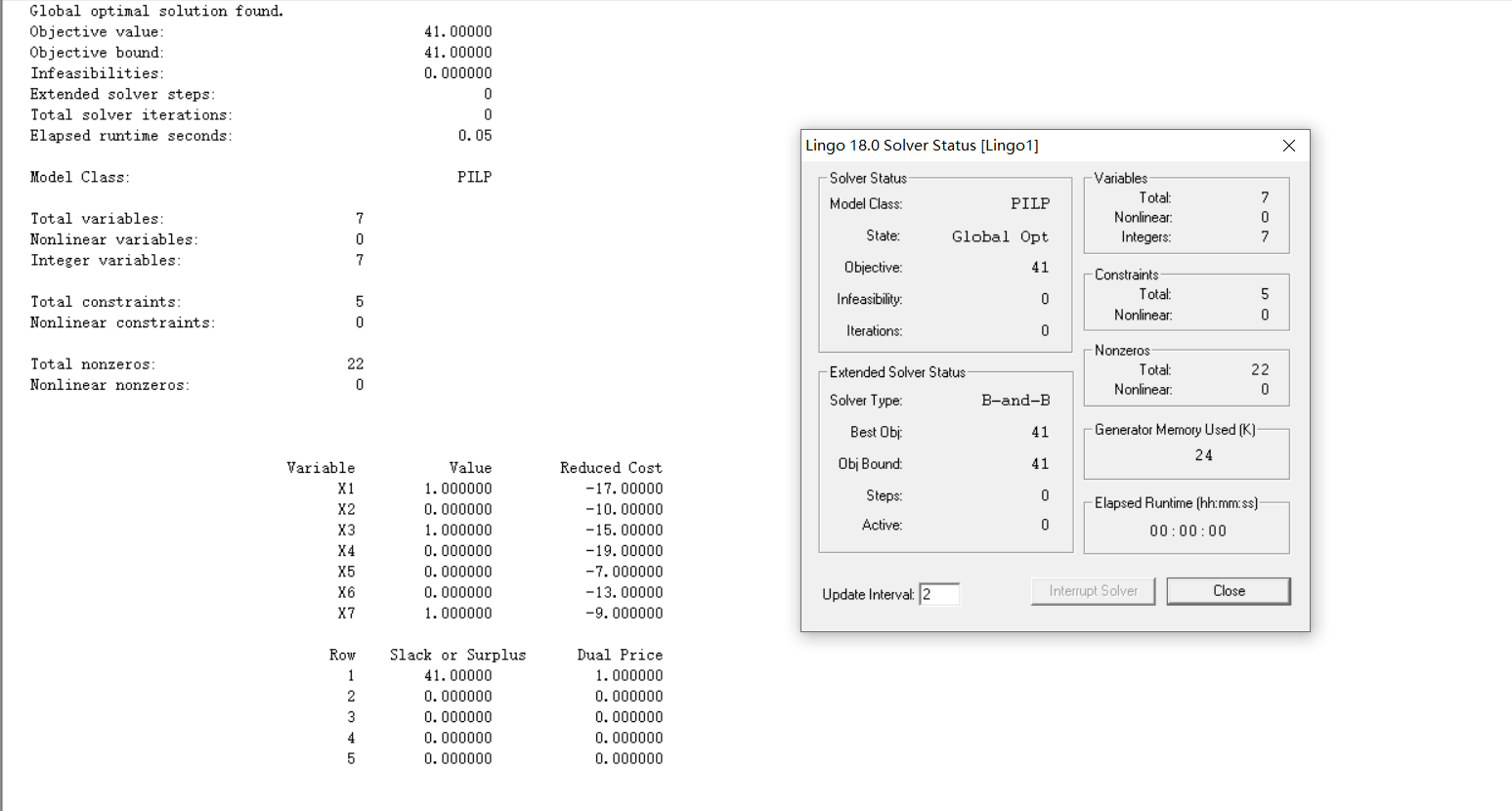
最优解：x1=x3=x7=1，其他为0

最大收益：41百万美金

MODEL:
max = 17*x1+10*x2+15*x3+19*x4+7*x5+13*x6+9*x7;
x1+x2<1;
x3+x4<1;
x3+x4<=x1+x2;
43*x1+28*x2+34*x3+48*x4+17*x5+32*x6+23*x7<=100;
@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);
end

(运输问题)设三个化肥厂供应四个地区的农用化肥，假设等量化肥在这些地区的使用效果相同,各个化肥厂的产量,需求地的需求量及各个化肥厂到需求低的单位运价见下表所示,现要求所有的化肥都要运送到四个地区，试求最佳调拨方案.

	B1	B2	B3	B4	产量
A1	16	13	22	17	50
A2	14	13	19	15	60
A3	19	20	23	—	50
最低需求	30	70	0	10
最高需求	50	70	30	不限

分析：

地区B4的最高需求是：当其他地区最低需求被满足时，供给给产B4的数量。

地区B4的最高需求=50+60+50-30-70=60

总产量=50+60+50=160

最低需求=30+70+10=110

最高需求=50+70+30+（160-30-70）=210

最大需求210比供应160多50,因此需要虚拟一个供应点A4，其供应量为50，使得供求平衡

	B1	B1~1~	B2	B3	B4	B4~1~	产量
A1	16	16	13	22	17	17	50
A2	14	14	13	19	15	15	60
A3	19	19	20	23	M	M	50
A4	M	0	M	0	M	0	50
需求	30	20	70	30	10	50

（M为任意大数，不会影响求最优解）

模型建立：

假设：

$x_{ij}$ 表示从化肥厂 $i$ 运送到地区 $j$ 的化肥数量。

目标是最小化总运输成本 $z$ ，即所有运输量与单位运价的乘积的总和。

模型的约束条件如下：

每个化肥厂的产量不能超过其最大产量。
每个地区的需求量必须得到满足。

最小化目标函数：

$z=\sum ^{4}_{i=1}\sum ^{6}_{j=1}c_{ij}x_{ij}$

其中， $c_{ij}$ 为化肥厂 $i$ 运送到地区 $j$ 的单位运价。

约束条件： $\sum ^{4}_{i=1}x_{ij}\leq F\left( i\right)$ ; $\sum ^{6}_{j=1}x_{ij}\geq M\left( j\right)$

MODEL:
sets:
	area/1..6/:M;
	factory/1..4/:F;
	link(factory,area):X,C;
endsets
data:
M = 30,20,70,30,10,50;
F = 50,60,50,50;
C = 16,16,13,22,17,17
14,14,13,19,15,15
19,19,20,23,1000,1000
1000,0,1000,0,1000,0;
enddata
min = @sum(link(i,j):X(i,j) * C(i,j));
@for(factory(i):@sum(area(j):X(i,j)) <= F(i));
@for(area(j):@sum(factory(i):X(i,j)) >= M(j));
end

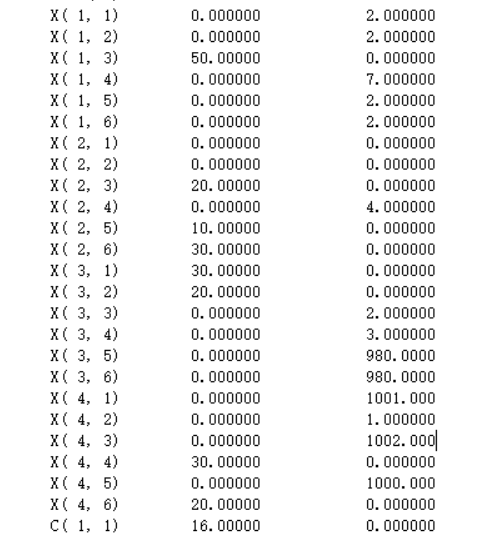
运算结果：

	B1	B1~1~	B2	B3	B4	B4~1~	产量
A1	0	0	50	0	0	0	50
A2	0	0	20	0	10	30	60
A3	30	20	0	0	0	0	50
A4	0	0	0	30	0	20	50
需求	30	20	70	30	10	50

	B1	B2	B3	B4	产量
A1	0	50*13	0	0	50
A2	0	20*13	0	40*15	60
A3	50*19	0	0	0	50
最低需求	30	70	0	10
最高需求	50	70	30	不限

总费用：50×13+20×13+40×15+50×19=2460